QUDT.org is a 501(c)(3) public charity nonprofit organization founded to provide semantic specifications for units of measure, quantity kind, dimensions and data types.   QUDT is an advocate for the development and implementation of standards to quantify data expressed in RDF and JSON.   Our mission is to improve interoperability of data and the specification of information structures through industry standards for Units of Measure, Quantity Kinds, Dimensions and Data Types.

QUDT.org operates thanks to volunteers, but we do have infrastructural costs of course. If you value the QUDT ontologies as a resource available to all, please consider a DONATION of any amount (tax deductible in the USA). That will allow us to keep going and growing.

Why QUDT.org

QUDT.org exists to make the QUDT Ontologies, derived models and vocabularies available to the public. Originally, QUDT models were developed for the NASA Exploration Initiatives Ontology Models (NExIOM) project, a Constellation Program initiative at the AMES Research Center (ARC).

Use Cases Benefitting From QUDT

QUDT is more than a set of vocabularies representing the various quantity and unit standards. It can be used to solve problems. Some of the associated use cases are itemized below:

• Conversion between single and complex unit types
• Dimensional analysis of equations
• Finding out equivalent units in different systems of units
• Finding out equivalent quantity kinds in different systems of quantities

Current Activities

Please see our Announcements Page on GitHub

QUDT BaseURIs

The DOI reference for citations of QUDT is: https://doi.org/10.25504/FAIRsharing.d3pqw7

QUDT is comprised of several linked ontologies. The core design pattern of the QUDT ontology is shown here:

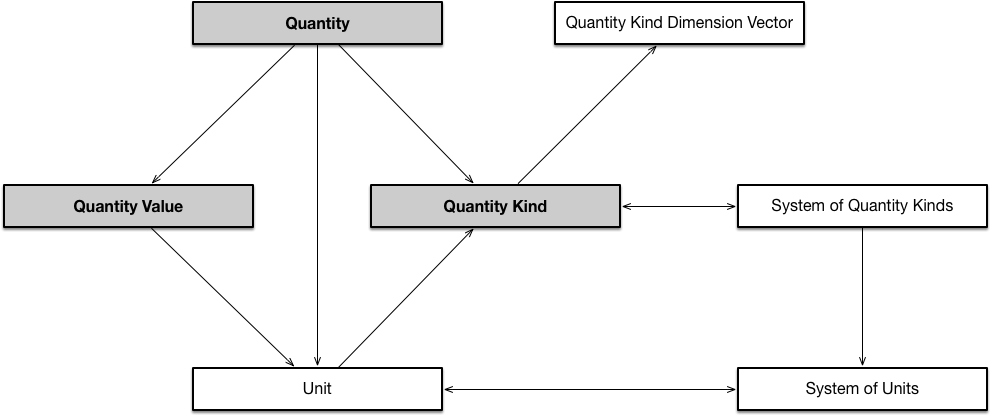
The table below provides the Base URIs for these ontologies.

Ontology	Base URI
Main QUDT Ontology	http://qudt.org/2.1/schema/qudt
QUDT Datatype Ontology	http://qudt.org/2.1/schema/datatype
QUDT Units Vocabulary	http://qudt.org/2.1/vocab/unit
QUDT QuantityKinds Vocabulary	http://qudt.org/2.1/vocab/quantitykind
QUDT DimensionVectors Vocabulary	http://qudt.org/2.1/vocab/dimensionvector
QUDT Physical Constants Vocabulary	http://qudt.org/2.1/vocab/constant
QUDT Systems of Units Vocabulary	http://qudt.org/2.1/vocab/sou
QUDT Systems of Quantity Kinds Vocabulary	http://qudt.org/2.1/vocab/soqk

Governance

QUDT is governed by a board of directors from different organizations.

Last Updated March 1, 2022

This work is licensed under a Creative Commons Attribution 4.0 International License.

---